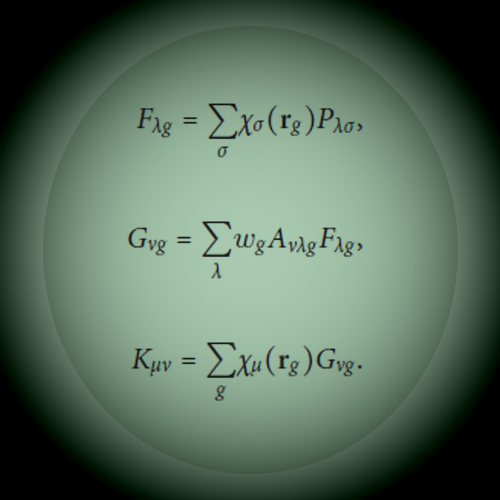Efficient low-scaling computation of NMR shieldings at the second-order Møller–Plesset perturbation theory level with Cholesky-decomposed densities and an attenuated Coulomb metric
2021-12-10
Michael Glasbrenner, Sigurd Vogler and Christian Ochsenfeld
J. Chem. Phys., 2021, 155, 224107
A method for the computation of nuclear magnetic resonance (NMR) shieldings with second-order Møller–Plesset perturbation theory (MP2) is presented which allows to efficiently compute the entire set of shieldings for a given molecular structure. The equations are derived using Laplace-transformed atomic orbital second-order Møller–Plesset perturbation theory as a starting point. The Z-vector approach is employed for minimizing the number of coupled-perturbed self-consistent-field equations that need to be solved. In addition, the method uses the resolution-of-the-identity approximation with an attenuated Coulomb metric and Cholesky decomposition of pseudo-density matrices. The sparsity in the three-center integrals is exploited with sparse linear algebra approaches, leading to reduced computational cost and memory demands. Test calculations show that the deviations from NMR shifts obtained with canonical MP2 are small if appropriate thresholds are used. The performance of the method is illustrated in calculations on DNA strands and on glycine chains with up to 283 atoms and 2864 basis functions